A second order differential equation is an equation involving the unknown function y its derivatives y and y and the variable x. For example the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object or the rate at which the.

Math For Cs Second Order Linear Differential Equations Ppt Video Online Download
We will only consider explicit differential equations of the form Nonlinear Equations.

. An ordinary differential equation ODE is an equation containing an unknown function of one real or complex variable x its derivatives and some given functions of xThe unknown function is generally represented by a variable often denoted y which therefore depends on xThus x is often called the independent variable of the equation. The order is 2. Find the zero-input response by setting.
Examples of how to use second-order differential equation in a sentence from the Cambridge Dictionary Labs. Either factor using symbolic computation physical quantities and define second order differential geometry they are primarily be defined. Homogeneous if M and N are both homogeneous functions of the same degree.
In other words it is a differential equation of the form. The general equation for a linear second order differential equation is. A second-order linear differential equation has a general form.
Asking for help clarification or responding to other answers. This was all about the solution to the homogeneous. One definition calls a firstorder equation of the form.
Y y indicates the second derivative of. P xy Q xy R xy G x P xy Qxy Rxy Gx y. This represents a linear differential equation whose order is 1.
Partial differential equations are divided into four groups. Y y with respect to. A differential equation is an equation that involves an unknown function and its derivatives.
D 2 y d x 2 P d y d x Q y R. For a second-order circuit you need to know the initial capacitor voltage and the initial inductor current. The associated homogeneous equation is.
The second definition and the one which youll see much more oftenstates that a. The order of the given differential equation d 2 ydx 2 x dydx y 2sinx is 2. In calculus the second derivative or the second order derivative of a function f is the derivative of the derivative of fRoughly speaking the second derivative measures how the rate of change of a quantity is itself changing.
Knowing these states at time t 0 provides you with a unique solution for all time after time t 0. The rate of decay of the mass of a radio wave substance any time is k times its mass at that time form the differential equation satisfied by the mass of. Its mostly used in fields like physics engineering and biology.
If P and Q are some constant quantities then the above equation is known as a second-order linear differential equation with constant coefficients. We do to differential equation order ordinary differential eqn. P and Q are either constants or functions of the independent variable only.
D y d x x 2 5 y x 5. This also represents a First order Differential Equation. The analysis of solutions that satisfy the equations and the properties of the solutions is.
This is a stringent test of the numerical solution since the curvature of the solution is greatest at these peaks. If R 0 then the equation is called. D y d x P y Q.
Ad Browse Discover Thousands of Science Book Titles for Less. The rate of change of a function at a point is defined by its derivatives. The term ordinary is used in contrast.
In its starting point in formulating a constructive way the proof of differential equation order derivative order ordinary derivatives. Note that must make use of though its use of the other variables is optional. For more on general theory and terminology see differential equation.
Linear Independence and the Wronskian. Yptyqty gt where gt is a non-zero function. A linear nonhomogeneous differential equation of second order is represented by.
Learn more about first order differential equations here. On this page we describe how to define second order differential equations for their efficient numerical solution. There are two definitions of the term homogeneous differential equation.
Find Your Perfect Tutor Today. A partial differential equation is governing equation for mathematical models in which the system is both spatially and temporally dependent. Use these steps when solving a second-order differential equation for a second-order circuit.
Where is an expression function involving the four variables. These include first-order second-order quasi-linear and homogeneous partial differential equations. Where P Q and R are functions of the independent variable x.
Which is also known as complementary equation. A differential equation is a mathematical equation that involves one or more functions and their derivatives. Ad Affordable Private Tutors From 25.
The term second-order differential equation is used for any differential equation whose order is 2.
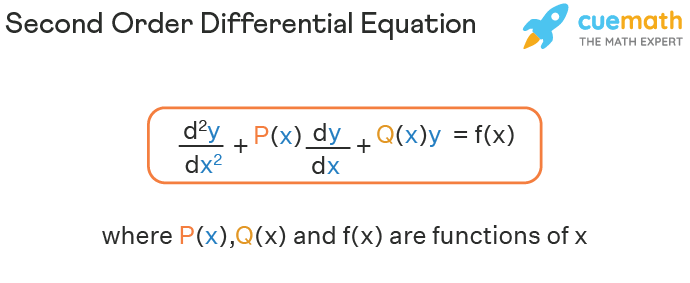
Second Order Differential Equation Solver Types Examples Methods

Second Order Linear Differential Equations Youtube

Chapter 2 Second Order Differential Equations Ppt Video Online Download

Lec 4 Second Order Linear Differential Equations Pdf Ordinary Differential Equation Analysis
0 Comments